Category: 算法

上期题目：矩阵翻转

解答：显然一个必要条件是两个矩阵里的元素必须是一致的，如果不一致可以直接判定不可能了。但这明显还不够。

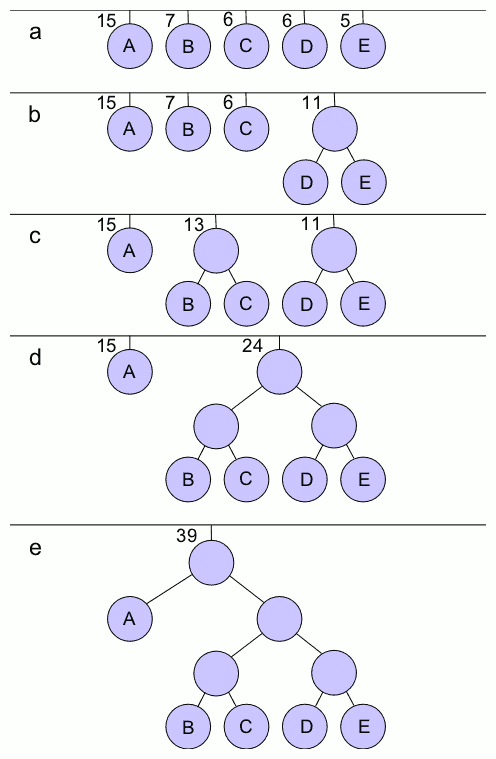
此类问题通常有一个入手点就是看看经过操作之后不变的是什么。对于本题，一个重要的观察是如果我们把矩阵如国际象棋棋盘一样黑白格交替染色，会发现翻转操作不会改变数字所在的格子颜色，黑格数永远是黑格数，白格数永远是白格数。那么自然的猜测就是，两个矩阵的黑格元素一致且白格元素一致，是不是可以成功的充分必要条件呢？

答案是肯定的，下面说一个不太正式的证明。实际上我们只需要2×2的翻转操作就可以达到目的。每次2×2翻转操作只交换了两个斜对角相邻的元素，我们可以想象把所有黑格拿出来排成一列，使得相邻的两个格子在原矩阵中是斜对角相邻的（对于非1xN或Nx1的矩阵总可以做到）。那么2×2翻转操作就是交换了序列里相邻的两个元素，显然通过这种交换我们可以得到任何一种可能的排列（想一下冒泡排序）。对白格同理。于是只要黑白格的元素分别是一致的，就一定可以达到。注意要特殊判断一下1xN的情况。

---

本期题目：大力出奇迹

我们都知道台球界有一句格言叫“大力出奇迹”（并没有），只要力气够大，总能把球蒙进去。下面从数学角度研究一下这个问题：在台球桌上放一个球，沿直线击出，球如果没有进洞就永远前进，撞到边后的反弹和光的反射一样入射角严格等于出射​角。球看作一个点，洞也看作点。

问题一：如果球永远不能进洞，那么一定是出现了循环么？（循环指以同一个方向回到以前经过的位置，比如平行于桌边轰一发，那么永远来回反弹）有没有可能不循环但是又永不进洞​？

问题二：假如随机选一个角度轰一发，球最终进洞的概率是多少？循环的概率是多少？

​问题三：存不存在一条永不进洞的线路，能经过桌面上任意一​点？

​问题四：稍微改一下设定，现在洞不是点，而是一个半径非常非常小的圆，当球和洞心的距离小于洞的半径时我们就认为球进洞​了。在这种情况下，随机选一个角度轰一发，球最终进洞的概率是多少？

这个其实是数学题，和算法没啥关系了，不过实在是很有意思所以发出来。来源记得是看到某篇公众号文章说的华尔街交易公司面试题，重新整理了一下。

上期问题 每期一题之3：猜对错

解答：

第一问比较容易，我们可以胡乱猜一个作为基准，比如就猜所有都是T。然后每轮仅把一题的答案改为F，看看新的结果和基准比是大了还是小了，大了说明这题应该是F，否则说明应该是T。这样用N+1轮得到所有结果。

想要仅用kN轮(k<1)有多种方法，基本思路是把题目每m个分成一组，每次用n轮提问确定m个答案(n<m)。下面是官方题解中用两轮确定三个答案的方案：

首先用两轮猜测TTTTTT…T和TFTFTF…TF作为基准一和基准二，设这两个基准值分别为x和y。我们把相邻三个题目作为一组，对于每一组，第一轮猜测时，以基准一为模版，只把对应组里前两题答案改为F，其他全不变。把结果与x值对比，那么有三种情况

1) 如果结果为x-2，说明前两题答案为TT。然后再简单用一轮提问确定第三题

2) 如果结果为x+2，说明前两题答案为FF。同样再用一轮确定第三题

3) 如果结果为x，说明前两题答案为TF或FT。此时，我们发起第二轮提问，这一次是以基准二为模版，把对应三道题的答案反转（不妨设本来是…TFT…，变成…FTF…），然后把结果与y值比较，那么我们会发现有四种情况：

3.1) 结果是y+3，说明这三题答案为FTF

3.2) 结果是y-3，说明这三题答案为TFT

3.3) 结果是y+1，说明前两题改对了，第三题改错了，这三题答案应为FTT

3.4) 结果是y-1，说明前两题改错了，第三题改对了，这三题答案应为TFF

综上，我们可以用每两轮搞定三题，外加两轮基准，还可能有最后一组不足三题的特殊处理。总之大约就是n*2/3轮查询。

第三问非常难，理论上说，总的可能性是2^n种，也就是n个比特的信息量。我们每轮询问得到一个数字n，即log(n)比特信息量，那么问题轮数的理论下界为O(n/log(n))次。这个下界是可以达到的，但是题解我看不懂……  题解可以点击下方“原文链接”查看，哪位看懂了可以给我解释一下。

---

本期题目：矩阵翻转

给定一个M*N的起始矩阵和一个M*N的目标矩阵，我们可以在起始矩阵上进行如下操作：选择一个K*K的子方阵(k<=M, k<=N)，把这个方阵的元素沿对角线翻转，注意可以沿两条对角线的任一条。问能否经过若干次操作，把起始矩阵变成目标矩阵。只需判断是否可以，不必输出具体过程。

例如，如果起始矩阵是[[1 2 3] [4 5 6]]，目标矩阵是[[1 4 3] [6 5 2]]，那么可以经过两次操作得到。先把右边2×2子方阵沿反对角线翻转，再把左边2×2子方阵沿主对角线翻转即可。

来源：Codechef August Long 2022, Angled Flip

上期题目：每期一题之2：猜数字

如果是均匀分布，直觉上就应该是类似二分搜索的方法，每次一定能把范围缩小一半。比如N=8时，第一轮先问是不是1<=N<=4，如果第一轮答是，第二轮则问是不是1<=N<=2；如果第一轮答否，第二轮问是不是5<=N<=6，依此类推。易知N=8时需要三轮。

当N较小时，有竞赛经验的同学可能容易想到一个“状态压缩动态规划”的算法。简单来说，对于一个集合S，我们可以设ans[S]表示已知结果一定在S之内的情况下，平均需要问多少次。那么我们最终要求的就是ans[{1,2,…N}]。这个东西可以递归来求，要计算ans[S]，我们可以枚举S的所有子集T来询问，我们用p[T]表示集合T中所有数的概率之和，那么我们有p[T]/p[S]的概率得到“是”的回答，然后我们递归求ans[T]；有1-p[T]/p[S]的概率得到“否”的回答，然后我们递归求ans[S-T]。写成方程式是这样的：

边界条件可以是当S中只有一个元素时，结果为0。

在递归的过程中我们可以把每个子集的结果记录下来防止重复计算，这个就是动态规划的思想。然而容易发现一共有2^N个状态，计算每个状态时也要枚举指数级别的子集，所以复杂度还是指数级，只能对比较小的N才可行，1000是绝不可能的。

实际上这题的最优解法是贪心。一个直观的思考方向是，如果一个数出现的概率越大，则应该花较少的步骤确定它，而比较罕见的数则可以用较多的步骤。实际上这个问题等价于Huffman编码问题，即给定一篇文档中每个字母出现的频率，给每个字母设定一个二进制编码，使得没有任何一个字母编码是另一个字母的前缀，要求文档的总编码长度最短。算法是逐次合并，一开始每个字母自己是一个集合，每个集合的权值就是字母频率。每次选出权值最低的两个集合，把它们合并起来，得到的新集合的权值为原来两个的权值和。这样重复操作直到只有一个集合。这个过程中就创建出一个二叉树，每个叶子节点是一个字母。我们给每个点的两条边分别标上0和1，这样每个字母的编码就得到了。

对应到本题，就是从二叉树的根开始，每次问是不是在一个子节点所对应的子集中，根据回答走向不同的分支。

正确性的证明可以用数学归纳法，这里就略过了，网上可以找到很多。算法用堆实现的话，复杂度是O(NlogN)。

---

本期题目：猜答案

试卷上面有N道判断题，你每次给出一组答案，我告诉你这次做对了几道，但不会告诉你具体是哪几道。你可以猜很多轮。设计一种方案用尽可能少的轮数做对所有的题。

比如有四道题，真正的答案是TTFF。你如果猜TFFF，我会告诉你对了3道。你如果猜FFTT，我会告诉你对了0道。真正的N会是一个比较大的数，比如几百道，所以乱蒙是效率太低的。

问题1：能否用大约N轮猜出？
问题2：能否用大约k*N轮猜出（k是一个小于1的常数）？
（附加题）问题3：能否用渐近意义上少于线性的轮数猜出？(用小o记号的话就是o(N)次)

题目来源：Codeforces #807 Div 2 Problem F