如果是均匀分布，直觉上就应该是类似二分搜索的方法，每次一定能把范围缩小一半。比如N=8时，第一轮先问是不是1<=N<=4，如果第一轮答是，第二轮则问是不是1<=N<=2；如果第一轮答否，第二轮问是不是5<=N<=6，依此类推。易知N=8时需要三轮。
当N较小时，有竞赛经验的同学可能容易想到一个“状态压缩动态规划”的算法。简单来说，对于一个集合S，我们可以设ans[S]表示已知结果一定在S之内的情况下，平均需要问多少次。那么我们最终要求的就是ans[{1,2,…N}]。这个东西可以递归来求，要计算ans[S]，我们可以枚举S的所有子集T来询问，我们用p[T]表示集合T中所有数的概率之和，那么我们有p[T]/p[S]的概率得到“是”的回答，然后我们递归求ans[T]；有1-p[T]/p[S]的概率得到“否”的回答，然后我们递归求ans[S-T]。写成方程式是这样的：
![ans[S]=1+\min_{T \subset S}(\frac{p[T]}{p[S]}ans[T] + \frac{p[S-T]}{p[S]}ans[S-T])](https://www.roba.ws/wp-content/ql-cache/quicklatex.com-ffb11bbcf62a28f2986d7538d3178b6e_l3.png "Rendered by QuickLaTeX.com")
边界条件可以是当S中只有一个元素时，结果为0。
在递归的过程中我们可以把每个子集的结果记录下来防止重复计算，这个就是动态规划的思想。然而容易发现一共有2^N个状态，计算每个状态时也要枚举指数级别的子集，所以复杂度还是指数级，只能对比较小的N才可行，1000是绝不可能的。
实际上这题的最优解法是贪心。一个直观的思考方向是，如果一个数出现的概率越大，则应该花较少的步骤确定它，而比较罕见的数则可以用较多的步骤。实际上这个问题等价于Huffman编码问题，即给定一篇文档中每个字母出现的频率，给每个字母设定一个二进制编码，使得没有任何一个字母编码是另一个字母的前缀，要求文档的总编码长度最短。算法是逐次合并，一开始每个字母自己是一个集合，每个集合的权值就是字母频率。每次选出权值最低的两个集合，把它们合并起来，得到的新集合的权值为原来两个的权值和。这样重复操作直到只有一个集合。这个过程中就创建出一个二叉树，每个叶子节点是一个字母。我们给每个点的两条边分别标上0和1，这样每个字母的编码就得到了。
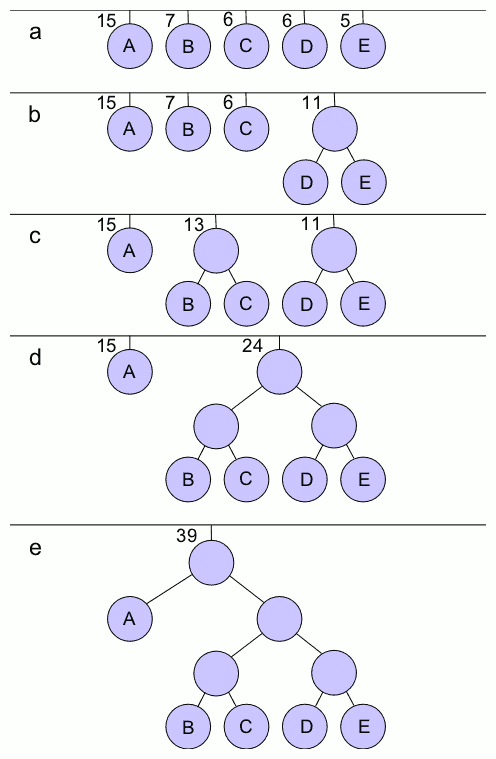
对应到本题，就是从二叉树的根开始，每次问是不是在一个子节点所对应的子集中，根据回答走向不同的分支。
正确性的证明可以用数学归纳法，这里就略过了，网上可以找到很多。算法用堆实现的话，复杂度是O(NlogN)。
本期题目：猜答案
试卷上面有N道判断题，你每次给出一组答案，我告诉你这次做对了几道，但不会告诉你具体是哪几道。你可以猜很多轮。设计一种方案用尽可能少的轮数做对所有的题。
比如有四道题，真正的答案是TTFF。你如果猜TFFF，我会告诉你对了3道。你如果猜FFTT，我会告诉你对了0道。真正的N会是一个比较大的数，比如几百道，所以乱蒙是效率太低的。
问题1：能否用大约N轮猜出？
问题2：能否用大约k*N轮猜出（k是一个小于1的常数）？
（附加题）问题3：能否用渐近意义上少于线性的轮数猜出？(用小o记号的话就是o(N)次)