说起分布式系统里的不可能性,大家第一反应应该是CAP理论。但是我们这篇不谈CAP,而是另一个关于共识算法的FLP定理。以后有机会的话再写写CAP以及这两个的关系。
FLP是三位作者的名字首字母。这个定理的内容是,在异步网络下,如果有一台机器可能出错,则没有任何确定性共识算法保证在有限时间内结束。这是一个相当强的结论,比起更著名的CAP理论,FLP不可能性定理实际上更不显然,也更有意思。
这里面有很多定义要首先明确:
- 异步网络。很不幸“异步”又是一个被滥用的词,在分布式系统理论中,异步网络指的是,系统中每个节点的执行速度不必一致,消息从一个节点传播到另一个节点的时间不确定,没有一个全局可见的准确时钟。在本论文的设定里,消息不会重复,不会丢失,只是可能会(有限)延迟。
- 出错。常见的出错类型有fail-stop, fail-recovery以及拜占庭错误。fail-stop指的是一台机器一旦出错就卡住不动了,fail-recovery指的是机器出错后会重启,从头开始执行,拜占庭错误指的是机器出错后进入混乱,可能乱给别人发消息,甚至是故意发误导性的消息(比如被黑客入侵了)。本论文里假定是fail-stop。
- 共识算法。本论文里讨论的是一个相当精简的共识问题:每个节点有一个初始值为0或1,经过一系列互相发消息沟通之后,每个节点都会做出一个决定,输出一个0或者一个1,一旦做出决定就不能再改。一个正确的共识算法要满足如下要求:
- 不同节点不能做出不一致的决定
- 需要在有限步数内完成
- 共识算法需要既有可能决定为0,也有可能决定为1。
(最后这一条是为了避免一种耍赖的方法,比如不管三七二十一通通决定0值,这样算法就没有意义。我后文把这一条称作“非trivial性”要求。)
下面我们把整个框架形式化一下,这个对于后面的证明是非常必要的:
我们的系统里有N个进程(N>=2),每个进程有一个1-bit的初始输入寄存器,有一个输出寄存器,取值为{b,0,1},一开始的时候值为b,表示尚未做出决定,在执行过程中这个输出值只可以写一次,写成0或1,表示相应的决定。每个进程还有自己的内部状态(aka内存)。
进程之间通过发消息交互。一条消息是一个(p,m)对,p表示消息的目标进程,m是消息内容。消息会放到一个统一的池子里,于是有两种操作:
– Send(p,m): 把消息(p,m)放到池子里
– Receive(p): 从池子里取一条发给p的消息,返回m给进程p,并把这条消息从池子里删除;或者返回一个空消息给进程p,注意即使这时池子里有给p的消息,也有可能不马上把这个消息给p,即模拟消息出现延迟的情况。但如果Receive(p)重复执行无限多次,所有给p的消息都会被p收到。
一个格局(原文是configuration,我瞎翻译的)指的是某一时刻所有进程的状态和消息池的状态的汇总。初始格局是每个进程只有输入寄存器非空,而所有进程内部状态和消息池都为空。算法执行过程就是连续从一个格局到另一个格局的转移,每次称为一步。每一步只涉及某单个进程p,先是执行Receive(p)得到一条发给p的消息或者空消息,然后进程p根据得到的消息和自己的内部状态,决定如何操作,包括改变自己的内部状态,放消息到消息池,和/或作出0/1决定。
注意我们讨论的是确定性共识算法,就是说一个格局C转变成什么新格局,是由从消息池取到什么消息唯一决定的。所以我们也把收到消息(p,m)称为一个事件e,用e(C)表示格局C经过事件e以后变成的新格局。我们把一系列连续的事件称为一个事件序列(原文是schedule,我又瞎翻的),常用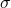 表示。
表示。
先说一个比较显然的引理:如果两个事件序列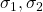 涉及的进程没有交集,那么从一个格局C先经过
涉及的进程没有交集,那么从一个格局C先经过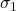 再经过
再经过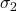 ,和先经过
,和先经过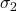 再经过
再经过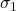 ,到达的是终点格局是相同的。这一点比较好理解,因为这两个序列涉及的是互不相关的进程,异步网络里不同进程收到消息的先后顺序本来就是不确定的,所以谁先谁后不应该对结果有任何影响。后文我把这个称做“交换律”。
,到达的是终点格局是相同的。这一点比较好理解,因为这两个序列涉及的是互不相关的进程,异步网络里不同进程收到消息的先后顺序本来就是不确定的,所以谁先谁后不应该对结果有任何影响。后文我把这个称做“交换律”。
 交换律示意图
交换律示意图下面开始真正的证明。我们用反证法,假设这样一个共识算法P存在,然后推导出矛盾。
对于一个格局C,如果因为之后发生的事件序列的不同,既有可能决定为0,也有可能决定为1,我们就称C为双值(bivalent)的。否则,就是不管后面事件序列怎样,都只能决定为0,就称为0-单值;如果只能决定为1,就称为1-单值。
下面我们简单证明,对于任何一个算法P来说,所有可能的初始格局里面一定存在双值格局。也就是说,总有某些初始格局你不能仅根据进程的初始输入就做出决定(比如在一个事先计算好的对应表里查,是不行的),而是要在算法的运行过程中根据消息的顺序不同而达到不同的最终决定。
我们用反证法,假设所有初始格局都是单值格局。因为非trivial性的要求,初始格局里需要即有0-单值格局又有1-单值格局。不妨设一共有N个进程,每个进程的初始输入为0或1,则初始格局共有2^N种。我们可以把这2^N个初始格局排成一列,使得相邻两个格局之间有且仅有一个进程的初始状态不同。这个东西叫做格雷码,总是可以构造出来的(详见Wiki)。比如三个进程的情况下,我们可以把8个初始格局排成000, 001, 011, 010, 110, 111, 101, 100。因为两种单值格局都有,那么序列里必然能找到相邻的两个初始格局属于不同的单值格局。而这相邻的两个格局只有一个进程的初始输入不同。如果刚好这个进程一开始就挂掉了没有任何响应,那么我们的共识算法没有任何办法区分这两种初始格局,也就不可能达成两种不同的最终决定。于是原引理成立。
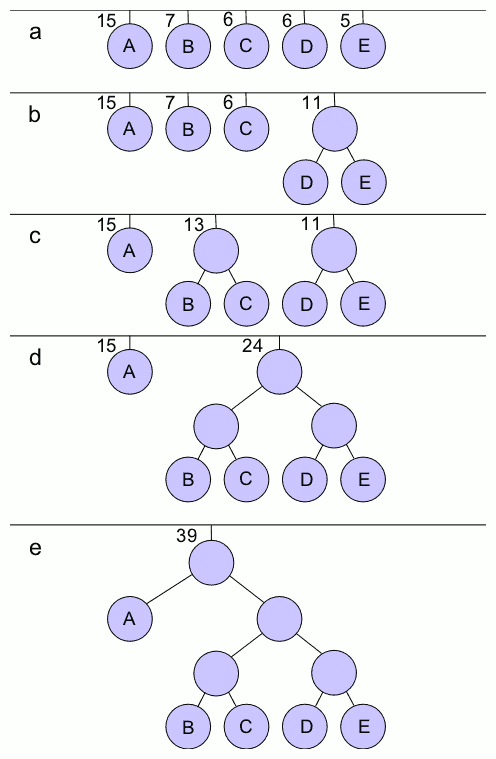
下面我们证明最重要的部分:设C是一个双值格局,事件e=(p,m)是一个可以发生在C上的事件。我们令ℂ表示从C格局出发不经过事件e可以达到的所有可能格局的集合,令D表示ℂ里面的每个格局都经过事件e得到的格局的集合,则D里一定仍包含双值格局。
这个描述有点绕,我们先看看如果它成立,能达成什么效果。前面引理已经证明了初始格局里一定有双值格局,我们拿一个这样的格局出来,再找一个接下来要发生的事件e,那么我们总可以通过把事件e推后到某个合适的时间发生,使得之后得到的格局仍然可能是双值格局(i.e.未能做出决定的格局)。从这个新双值格局继续同样操作,那么就可以永远留在双值格局,不做出最终决定。这样这个共识算法就不能终止了。
还是用反证法,假设D里不包含双值格局,我们试图推出矛盾。
若D不包含双值格局,我们可以得出D里必须两种单值格局都存在。(1)
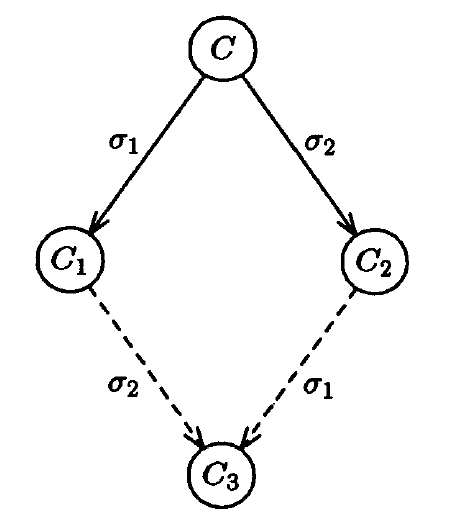
这一步的证明是这样的:因为初始格局C是双值的,那么一个存在一个0-单值格局E0和一个1-单值格局E1可以从C到达。我们先看E0,一种可能是E0属于ℂ集合,那么F0=e(E0)就属于D集合,显然F0也是0-单值的;另一种可能是E0不属于ℂ集合,这时一定在D里存在一个F0使得从F0可以到达E0,因为D里只有单值格局,那么F0一定是0-单值的。综合两种情况,D集合里必然有0-单值格局。同样的逻辑对E1也成立,所以D集合里也必然有1-单值格局。故(1)得证。
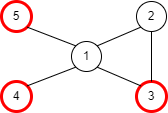
简化一点来说就是,对于E0,我们一定能在D里找到一个单值格局F0,使得要么能从E0到F0,要么能从F0到E0。下面这个盗来的图形象描绘了这一部分证明:
 来源:https://www.the-paper-trail.org/post/2008-08-13-a-brief-tour-of-flp-impossibility/
来源:https://www.the-paper-trail.org/post/2008-08-13-a-brief-tour-of-flp-impossibility/
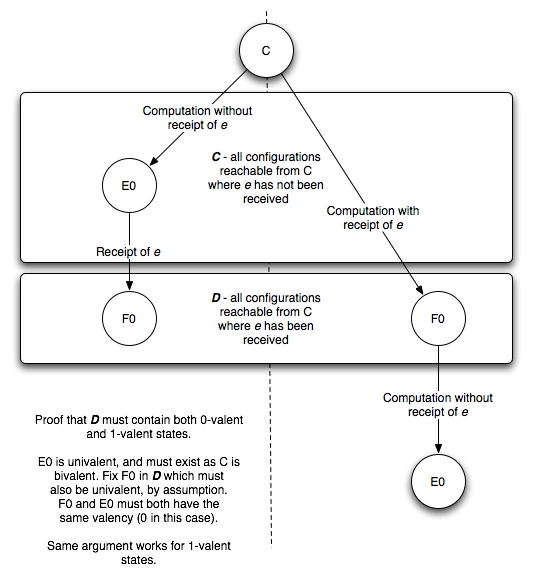
现在我们知道D里面两种单值格局都有了,因为D里的每个格局都是从ℂ里的某个格局经过一步e得到的,那么我们一定能在ℂ里找到相邻的两个格局C0,C1,使得D0=e(C0)是0-单值格局,而D1=e(C1)是1-单值格局。不妨设�是C0经过一步e’得到C1。(若则C1经过一步到C0下面的讨论也同样成立)
此时对e’=(p’,m’)有两种情况,
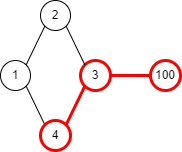
情况一:若p’不等于p,也就是说e和e’是作用在不同的节点上的。那么根据交换律,交换e和e’的顺序结果应该不变。我们已经知道了C0通过e’到达C1再通过e到达D1。还知道C0通过e到达D0,此时如果让D0接受事件e’,因为满足交换律我们应该也得到D1。但这是不可能的因为D0已经是单值格局不能变了,所以得出矛盾。见下图:
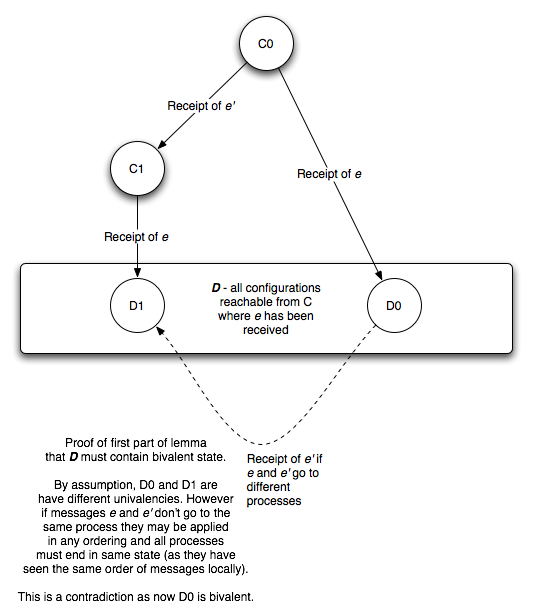 来源:https://www.the-paper-trail.org/post/2008-08-13-a-brief-tour-of-flp-impossibility/
来源:https://www.the-paper-trail.org/post/2008-08-13-a-brief-tour-of-flp-impossibility/
情况二:若p’等于p,此时从C0出发必存在一个不涉及节点p的事件序列R,能达到一个单值格局A。(因为我们的算法要在有一个节点挂了的时候仍能正常运行,现在就好比是p点挂了)现在我们让D0接到序列R,设结果为E0,也就是说E0=R(e(C0))。因为R不涉及p,根据交换律,我们让A接收事件e后,也应该得到E0,也就是e(A)=e(R(C0))=R(e(c0))=E0。类似地,我们让D1接受序列得到E1,也就是说E1=R(e(e'(C0))),同样根据交换律,A接收事件e和e’后也应该得到E1,e(e'(A)) = e(e'(R(C0))=R(e(e'(C0)))=E1。但是,A已经是单值格局了,不可能既能到E0又能到E1,得出矛盾。
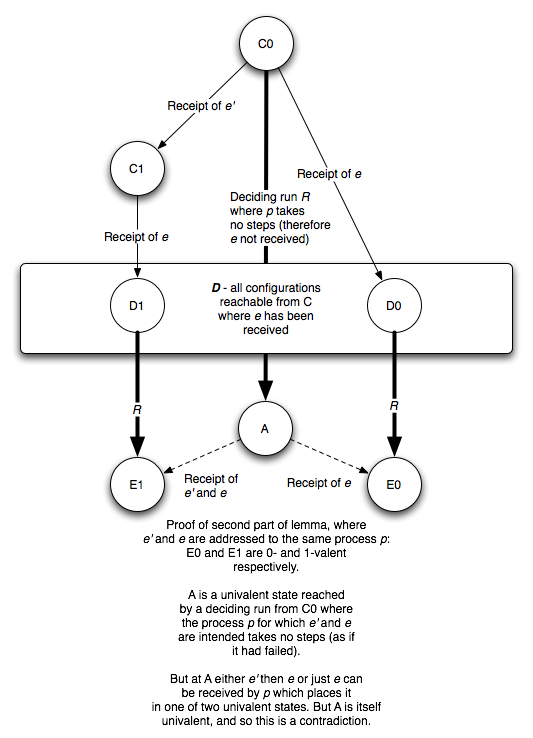 来源:https://www.the-paper-trail.org/post/2008-08-13-a-brief-tour-of-flp-impossibility/
来源:https://www.the-paper-trail.org/post/2008-08-13-a-brief-tour-of-flp-impossibility/
综合以上所有这些矛盾,说明我们一开始的假设“D里不包含双值格局”是不正确的。D里必定包含双值格局。所以我们前面说的这个构造无限序列的方法就成立了:
前面引理已经证明了初始格局里一定有双值格局,我们拿一个这样的格局出来,再找一个接下来要发生的事件e,那么我们总可以通过把事件e推后到某个合适的时间发生,使得之后得到的格局仍然可能是双值格局(i.e.未能做出决定的格局)。从这个新双值格局继续同样操作,那么就可以永远留在双值格局,不做出最终决定。这样这个共识算法就不能终止了。
所以原始的命题得证:在异步网络中,只要有一个节点有可能挂,理论上就不存在一定能在有限时间内结束的共识算法。
总结
这个结论是出乎意料的强,所以这篇论文获得了广泛的赞誉。给人的第一感觉是,这么一点点小错误都不让发生,分布式系统还能有个啥卵用。 实际上也并不需要那么悲观,因为真正的网络不可能是完全异步的,这种陷入无限循环可能性微乎其微。后续的很多研究是把“完全异步”这一条件放宽一点点,然后就有很多可以做到的事情了。如果以后有时间我可以写写后续。
论文原文:https://groups.csail.mit.edu/tds/papers/Lynch/jacm85.pdf
参考资料:https://www.the-paper-trail.org/post/2008-08-13-a-brief-tour-of-flp-impossibility/